无锁HashMap的原理与实现
(本文由onetwogoo投稿)
在《疫苗:Java HashMap的死循环》中,我们看到,java.util.HashMap并不能直接应用于多线程环境。对于多线程环境中应用HashMap,主要有以下几种选择:
- 使用线程安全的java.util.Hashtable作为替代。
- 使用java.util.Collections.synchronizedMap方法,将已有的HashMap对象包装为线程安全的。
- 使用java.util.concurrent.ConcurrentHashMap类作为替代,它具有非常好的性能。
而以上几种方法在实现的具体细节上,都或多或少地用到了互斥锁。互斥锁会造成线程阻塞,降低运行效率,并有可能产生死锁、优先级翻转等一系列问题。
CAS(Compare And Swap)是一种底层硬件提供的功能,它可以将判断并更改一个值的操作原子化。关于CAS的一些应用,《无锁队列的实现》一文中有很详细的介绍。
目录
Java中的原子操作
在java.util.concurrent.atomic包中,Java为我们提供了很多方便的原子类型,它们底层完全基于CAS操作。
例如我们希望实现一个全局公用的计数器,那么可以:
private AtomicInteger counter = new AtomicInteger(3);
public void addCounter() {
for (;;) {
int oldValue = counter.get();
int newValue = oldValue + 1;
if (counter.compareAndSet(oldValue, newValue))
return;
}
}
其中,compareAndSet方法会检查counter现有的值是否为oldValue,如果是,则将其设置为新值newValue,操作成功并返回true;否则操作失败并返回false。
当计算counter新值时,若其他线程将counter的值改变,compareAndSwap就会失败。此时我们只需在外面加一层循环,不断尝试这个过程,那么最终一定会成功将counter值+1。(其实AtomicInteger已经为常用的+1/-1操作定义了incrementAndGet与decrementAndGet方法,以后我们只需简单调用它即可)
除了AtomicInteger外,java.util.concurrent.atomic包还提供了AtomicReference和AtomicReferenceArray类型,它们分别代表原子性的引用和原子性的引用数组(引用的数组)。
无锁链表的实现
在实现无锁HashMap之前,让我们先来看一下比较简单的无锁链表的实现方法。
以插入操作为例:
- 首先我们需要找到待插入位置前面的节点A和后面的节点B。
- 然后新建一个节点C,并使其next指针指向节点B。(见图1)
- 最后使节点A的next指针指向节点C。(见图2)
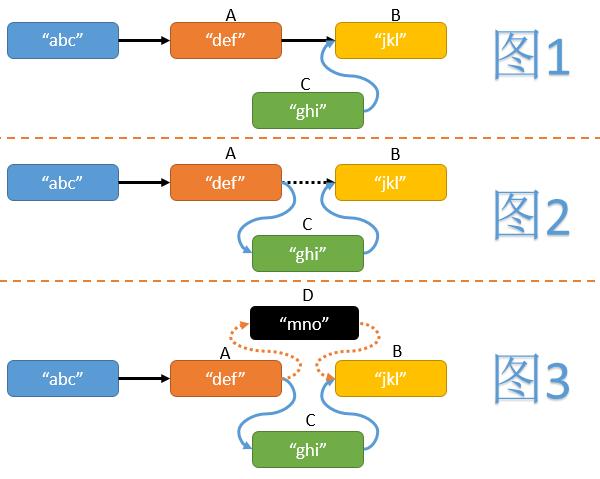
但在操作中途,有可能其他线程在A与B直接也插入了一些节点(假设为D),如果我们不做任何判断,可能造成其他线程插入节点的丢失。(见图3)我们可以利用CAS操作,在为节点A的next指针赋值时,判断其是否仍然指向B,如果节点A的next指针发生了变化则重试整个插入操作。大致代码如下:
private void listInsert(Node head, Node c) {
for (;;) {
Node a = findInsertionPlace(head), b = a.next.get();
c.next.set(b);
if (a.next.compareAndSwap(b,c))
return;
}
}
(Node类的next字段为AtomicReference<Node>类型,即指向Node类型的原子性引用)
无锁链表的查找操作与普通链表没有区别。而其删除操作,则需要找到待删除节点前方的节点A和后方的节点B,利用CAS操作验证并更新节点A的next指针,使其指向节点B。
无锁HashMap的难点与突破
HashMap主要有插入、删除、查找以及ReHash四种基本操作。一个典型的HashMap实现,会用到一个数组,数组的每项元素为一个节点的链表。对于此链表,我们可以利用上文提到的操作方法,执行插入、删除以及查找操作,但对于ReHash操作则比较困难。
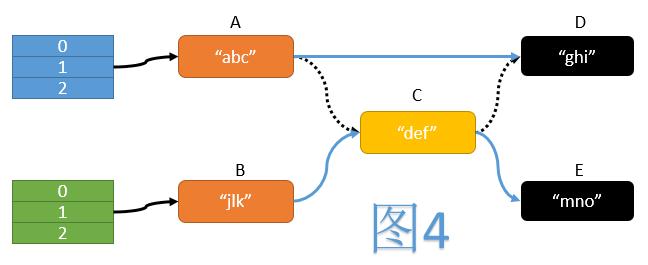
如图4,在ReHash过程中,一个典型的操作是遍历旧表中的每个节点,计算其在新表中的位置,然后将其移动至新表中。期间我们需要操纵3次指针:
- 将A的next指针指向D
- 将B的next指针指向C
- 将C的next指针指向E
而这三次指针操作必须同时完成,才能保证移动操作的原子性。但我们不难看出,CAS操作每次只能保证一个变量的值被原子性地验证并更新,无法满足同时验证并更新三个指针的需求。
于是我们不妨换一个思路,既然移动节点的操作如此困难,我们可以使所有节点始终保持有序状态,从而避免了移动操作。在典型的HashMap实现中,数组的长度始终保持为2i,而从Hash值映射为数组下标的过程,只是简单地对数组长度执行取模运算(即仅保留Hash二进制的后i位)。当ReHash时,数组长度加倍变为2i+1,旧数组第j项链表中的每个节点,要么移动到新数组中第j项,要么移动到新数组中第j+2i项,而它们的唯一区别在于Hash值第i+1位的不同(第i+1位为0则仍为第j项,否则为第j+2i项)。
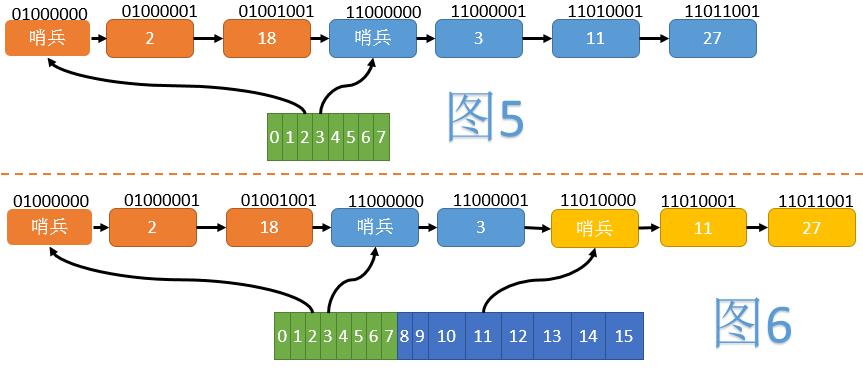
如图5,我们将所有节点按照Hash值的翻转位序(如1101->1011)由小到大排列。当数组大小为8时,2、18在一个组内;3、11、27在另一个组内。每组的开始,插入一个哨兵节点,以方便后续操作。为了使哨兵节点正确排在组的最前方,我们将正常节点Hash的最高位(翻转后变为最低位)置为1,而哨兵节点不设置这一位。
当数组扩容至16时(见图6),第二组分裂为一个只含3的组和一个含有11、27的组,但节点之间的相对顺序并未改变。这样在ReHash时,我们就不需要移动节点了。
实现细节
由于扩容时数组的复制会占用大量的时间,这里我们采用了将整个数组分块,懒惰建立的方法。这样,当访问到某下标时,仅需判断此下标所在块是否已建立完毕(如果没有则建立)。
另外定义size为当前已使用的下标范围,其初始值为2,数组扩容时仅需将size加倍即可;定义count代表目前HashMap中包含的总节点个数(不算哨兵节点)。
初始时,数组中除第0项外,所有项都为null。第0项指向一个仅有一个哨兵节点的链表,代表整条链的起点。初始时全貌见图7,其中浅绿色代表当前未使用的下标范围,虚线箭头代表逻辑上存在,但实际未建立的块。
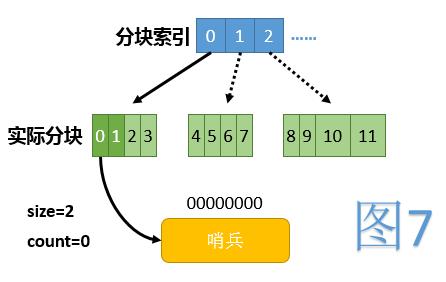
初始化下标操作
数组中为null的项都认为处于未初始化状态,初始化某个下标即代表建立其对应的哨兵节点。初始化是递归进行的,即若其父下标未初始化,则先初始化其父下标。(一个下标的父下标是其移除最高二进制位后得到的下标)大致代码如下:
private void initializeBucket(int bucketIdx) {
int parentIdx = bucketIdx ^ Integer.highestOneBit(bucketIdx);
if (getBucket(parentIdx) == null)
initializeBucket(parentIdx);
Node dummy = new Node();
dummy.hash = Integer.reverse(bucketIdx);
dummy.next = new AtomicReference<>();
setBucket(bucketIdx, listInsert(getBucket(parentIdx), dummy));
}
其中getBucket即封装过的获取数组某下标内容的方法,setBucket同理。listInsert将从指定位置开始查找适合插入的位置插入给定的节点,若链表中已存在hash相同的节点则返回那个已存在的节点;否则返回新插入的节点。
插入操作
- 首先用HashMap的size对键的hashCode取模,得到应插入的数组下标。
- 然后判断该下标处是否为null,如果为null则初始化此下标。
- 构造一个新的节点,并插入到适当位置,注意节点中的hash值应为原hashCode经过位翻转并将最低位置1之后的值。
- 将节点个数计数器加1,若加1后节点过多,则仅需将size改为size*2,代表对数组扩容(ReHash)。
查找操作
- 找出待查找节点在数组中的下标。
- 判断该下标处是否为null,如果为null则返回查找失败。
- 从相应位置进入链表,顺次寻找,直至找出待查找节点或超出本组节点范围。
删除操作
- 找出应删除节点在数组中的下标。
- 判断该下标处是否为null,如果为null则初始化此下标。
- 找到待删除节点,并从链表中删除。(注意由于哨兵节点的存在,任何正常元素只被其唯一的前驱节点所引用,不存在被前驱节点与数组中指针同时引用的情况,从而不会出现需要同时修改多个指针的情况)
- 将节点个数计数器减1。